The Comprehensive Care Provided by Plastic Surgeons
A medical professional who performs plastic surgery must undergo rigorous training to become a member of the American Board of Plastic Surgery. This includes a medical degree, surgical residency and plastic surgery fellowship.
In trauma bays, plastic surgery services often interact with other surgical specialties to manage cases with exposed skeleton or orthopedic hardware. Small upper extremity-related cases were also common submissions to plastic surgery.
Cosmetic
Many patients are confused by the terms “reconstructive surgery” and “cosmetic surgery.” Generally speaking, plastic surgeons perform both reconstructive procedures to restore function and normal appearance as well as cosmetic enhancements.
When choosing a surgeon, it is important to check the doctor’s credentials and make sure they have completed an accredited residency training program specifically in plastic surgery. A comprehensive training program will have taught the surgeon the full spectrum of reconstructive and cosmetic procedures.
A good plastic surgeon, certified by the American Board of Plastic Surgery, such as those at Dr Dean White (deanwhite.com.au), provides assurance that the surgeon has completed a year of additional fellowship training in cosmetic surgery, including facial, breast, and body procedures.
Before cosmetic surgery, the surgeon will review a patient’s medical history to evaluate any health concerns that might affect their surgical results. They will also discuss the desired outcome of the procedure. This is an opportunity for the patient to ask any questions they may have and for the surgeon to explain the process of achieving that result.
Depending on the patient’s health, the type of surgery and their desired outcome, some cosmetic procedures may be performed in a freestanding surgical facility or the physician’s office under local anesthesia. Often times, these procedures require some time to heal, and it is important that the patient prepare by understanding what to expect afterward, such as bruising and swelling.
Reconstructive
For patients who have suffered severe injuries to parts of their bodies, plastic surgeons can reconstruct damaged tissues to provide function and a normal appearance. These surgical procedures may involve skin, muscle, bone or tendons. Some of these reconstructive surgeries may be performed through a technique called tissue-based reconstruction, in which surgeons use a patient’s own body tissue (such as skin from the belly) to reconstruct a part of the patient’s body. This helps reduce damage to the donor site, improves surgical results and decreases rates of complications.
Many health plans cover reconstructive procedures that have been deemed medically necessary. This is unlike cosmetic procedures, which are not typically covered by insurance.
This includes treating congenital conditions like cleft lips and palates, craniofacial abnormalities, hypospadias and other genito-urinary defects; trauma to the face, skeleton, trunk and limbs; burn wound care; and complex wound reconstruction using free flaps and skin grafts. In addition, plastic surgeons are often involved in level 1 trauma centers where they perform a variety of reconstructive procedures including skeletal injury management, limb-saving free tissue transfers and complex wound repair.
Many of these procedures are interdisciplinary and require coordination with physicians from other specialties. For example, four of our plastic surgeons at Nationwide Children’s Hospital are trained in velopharyngeal dysphagia (VPD), a condition that affects the network of nerves that control arm and shoulder/hand function. This condition can result from birth trauma or later injury and causes difficulty in breathing, swallowing and speaking.

Head & Neck
For patients who have had cancer of the head or neck, reconstructive plastic surgery can repair the damage caused by the removal of a tumor, preserving as much function as possible. At MSK, our head and neck surgeons work closely with plastic surgeons to offer a coordinated care experience that enhances patients’ ability to function normally.
In addition to repairing skin damage and restoring a patient’s appearance, head and neck reconstruction surgery can restore function that was lost during tumor removal or prior radiotherapy treatment. For example, if a facial bone has been removed as part of radiation treatment for a tumor, the plastic surgeon can rebuild the bone using pedicled or free flaps, alloplasts, and/or grafts.
Medical students, residents, and fellows learn innovative three-dimensional planning techniques and surgical procedures for head and neck reconstruction to optimize both function and physical appearance. They also participate in a multidisciplinary clinic where they can evaluate and treat head, neck, thyroid, and upper aerodigestive tract benign and malignant tumors and abnormalities in a high-volume setting.
In addition, our surgeons have expertise in skull-base tumors including sinonasal carcinoma and nasopharyngeal carcinoma. They use a minimally invasive technique called transnasal endoscopy, which allows them to remove these tumors without the need for open surgery and with fewer complications. Patients with these tumors can often return home the day of or the day after their procedure.
Body
Surgical procedures that improve and enhance body contours include reduction mammaplasty (breast surgery), abdominoplasty (“tummy tuck”), liposuction, rhinoplasty (“nose job”), and otoplasty (“ear surgery”/”ear pinning”). Other body procedures can help you feel more confident about the way you look by restoring your body’s proportional balance.
When you meet with a plastic surgeon, your doctor will discuss your goals and explain the procedure in detail. You’ll also learn about recovery, including home care instructions and what to expect during your healing process. Your doctor will also explain the concept of asymmetry — how one side of your face or body looks naturally different from the other — and might recommend additional cosmetic procedures to achieve greater balance.
Plastic surgeons are uniquely trained to provide both reconstructive and cosmetic services for all parts of the body. They are also experts in craniofacial surgery, microsurgery and hand surgery. In addition, they have extensive experience in the treatment of burns. Research has shown that patients who are seen by plastic surgeons at level I trauma centers have better outcomes than those who do not.

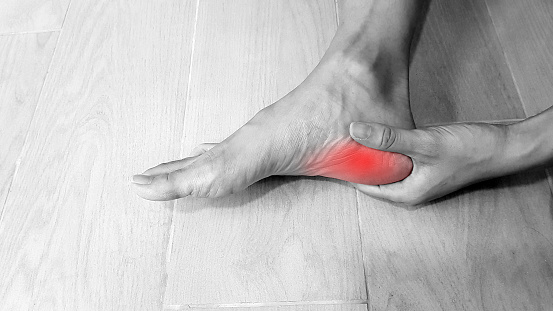
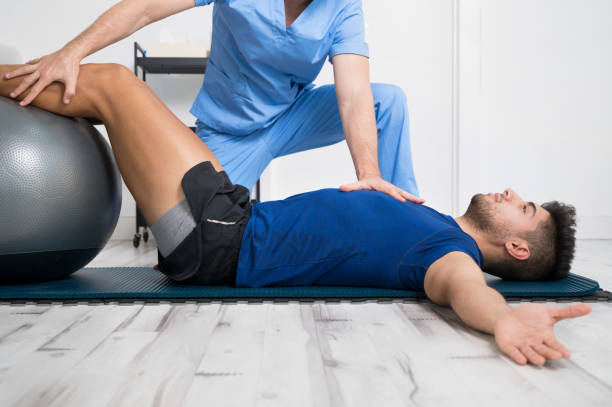


 Physiotherapists near Thornbury are professionals who are skilled in treating movement-impairing diseases such as arthritis. They can treat both acute and chronic conditions and are skilled in treating a variety of different sports injuries, such as torn muscles, sprains, and strains. Some physios specialize in rehabilitation, while others are specialized in sports medicine. There are numerous different types of physios. Each type of physio is qualified to treat a specific type of patient and comes with an educational background and experience in treating that particular type of patient.
Physiotherapists near Thornbury are professionals who are skilled in treating movement-impairing diseases such as arthritis. They can treat both acute and chronic conditions and are skilled in treating a variety of different sports injuries, such as torn muscles, sprains, and strains. Some physios specialize in rehabilitation, while others are specialized in sports medicine. There are numerous different types of physios. Each type of physio is qualified to treat a specific type of patient and comes with an educational background and experience in treating that particular type of patient.