Recovery Techniques in Sports Physiotherapy
In order to achieve high performance, athletes push their bodies to the limits during training and competition. However, making time for recovery is crucial to ensure long-term gains in fitness levels.
This article explores several easy-to-follow recovery techniques to help reduce muscle soreness, increase recovery and aid injury prevention.
Rest
As an athlete, you know that proper recovery techniques are vital to achieving your training and competition goals. Whether you’re recovering from an injury or looking to improve your performance, these recovery techniques can help you resume training and competition feeling rejuvenated.
The sports physio Canberra techniques used in sports recovery focus on reducing muscle soreness and improving flexibility, without adding additional strain to the body. These include active recovery, stretching, hydrotherapy, and compression garments.
During the immediate recovery phase, athletes should focus on cooling down and refueling their bodies. They can also use ice therapy to reduce inflammation and help the muscles heal faster. Athletes should incorporate stretching into their recovery routines, as this can increase blood flow and reduce muscle soreness. They can also use foam rolling and massage to speed up the healing process.
Ice
As an athlete, you push your body to its limits. It’s important to take time to rest and recover so you can keep up with your training. Without proper recovery techniques, you can get injured and experience a decline in performance.
Cold water immersion (CWI) is an effective recovery technique that can reduce inflammation, soreness, and fatigue. It can be performed before or after high-intensity workouts or competitions.
Active recovery is a low-intensity exercise used by athletes to flush out waste, improve circulation, and reduce muscle soreness. It is best performed on rest days, and can include activities like walking, swimming, and cycling.
Stretching is an important component of any athletic recovery routine, and should be done regularly to maintain flexibility and prevent injury. It is best performed after each workout, and can include dynamic and static stretching to target specific muscles based on training intensity and goals.
Compression
High-performance athletes rely on recovery techniques to ensure that they can return to peak performance after workouts and competitions. These techniques are critical for minimizing fatigue, muscle injury, and optimizing the body’s physical conditioning.
Compression is an important recovery technique in sports physiotherapy to reduce swelling and increase blood flow to the injured area. This improves lymph fluid circulation, which helps transport metabolic waste away from the injured tissue. It also improves the flow of oxygen-rich blood to the injury, which promotes healing.
Stretching is another common recovery technique, but research on its effectiveness is inconsistent. A study by Kinugasa and Kilding found that stretching did not significantly improve recovery from a game of basketball.
Elevation
For athletes, achieving the appropriate balance between training and recovery is critical to maximize performance. Achieving this balance requires a combination of several recovery techniques, including rest, ice, compression and elevation.
Elevation helps reduce swelling by preventing the pooling of fluid in injured joints and muscles. This helps decrease pain, improves range of motion and speed up healing.
Physiotherapists also use advanced manual therapies like instrument-assisted soft tissue mobilization (IASTM) to break down adhesions and scar tissue that limit mobility. They can also advise athletes on injury prevention strategies, such as stretching, which improves flexibility and prevents muscle imbalances that lead to injuries. They can also teach athletes about proper warm-up and cool-down routines to avoid injury and improve performance.
Active recovery
Whether they are professional athletes or just playing for fun, sportspeople place a huge strain on their bodies. They need to train hard in order to improve their performance, but they also need to recover well to prevent injury and avoid fatigue.
Active recovery involves low-intensity exercise to keep muscles moving and increase blood flow. Studies have shown that it can reduce muscle soreness and enhance recovery. It can also help athletes achieve physiological homeostasis more quickly than passive recovery.
Some examples of active recovery include walking, swimming, and light cardio. Stretching exercises are another common part of this recovery technique. These can make muscles more flexible and help prevent injuries. In addition, they can also help athletes maintain their strength during recovery days.
Hydrotherapy
Using hydrotherapy techniques can improve circulation, reduce muscle soreness and promote relaxation. It can also help reduce the risk of injury and enhance performance in athletes.
The physiologic effects of water, including buoyancy and hydrostatic pressure, make it an excellent mode of exercise for those with orthopedic or musculoskeletal limitations, as well as for those who are overweight or have heart failure. It can also be beneficial for those who experience pain from ankylosing spondylitis, psoriatic arthritis or osteoarthritis.
Stretching is another important recovery technique. It helps improve flexibility, reduce muscle stiffness and prevent injuries. Incorporate regular stretching into your workout routine to boost recovery and enhance sports performance. Physiotherapists can also teach you proper stretching techniques and help you develop a routine that fits your lifestyle.
Manual therapies
Manual therapy is a hands-on technique used to assess and treat musculoskeletal injuries and dysfunctions. The goal is to restore optimum body function, mobility and strength. This can improve performance and reduce injury risk.
This type of therapy consists of techniques such as soft tissue manipulation and joint mobilization. They can increase the range of motion of a stiff joint and decrease pain, swelling and irritability. It can also help stretch tight muscles and release endorphins.
The best part is that it’s a safe and effective way to relieve pain! If you’re suffering from chronic pain, contact us at Powerhouse Physiotherapy today to schedule an appointment. Our dedicated physical therapists are ready to assist you. We look forward to helping you get back to your normal life!


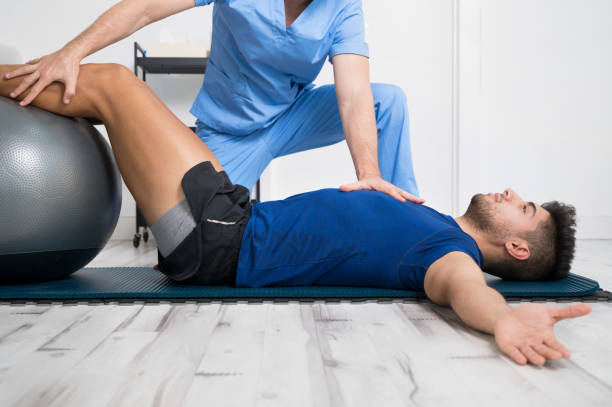


 Physiotherapists near Thornbury are professionals who are skilled in treating movement-impairing diseases such as arthritis. They can treat both acute and chronic conditions and are skilled in treating a variety of different sports injuries, such as torn muscles, sprains, and strains. Some physios specialize in rehabilitation, while others are specialized in sports medicine. There are numerous different types of physios. Each type of physio is qualified to treat a specific type of patient and comes with an educational background and experience in treating that particular type of patient.
Physiotherapists near Thornbury are professionals who are skilled in treating movement-impairing diseases such as arthritis. They can treat both acute and chronic conditions and are skilled in treating a variety of different sports injuries, such as torn muscles, sprains, and strains. Some physios specialize in rehabilitation, while others are specialized in sports medicine. There are numerous different types of physios. Each type of physio is qualified to treat a specific type of patient and comes with an educational background and experience in treating that particular type of patient.